Логнормальное распределение

Неотрицательная случайная величина X называется распределенной логарифмически нормально, если ее логарифм Z = lg X распределен по нормальному закону. Логарифмическим нормальным распределением, как правило, хорошо аппроксимируются такие случайные величины X, которые образуются в результате умножения большого числа независимых или слабо зависимых неотрицательных случайных величин, дисперсия каждой из которых мала по сравнению с дисперсией их суммы.

Область x	0 < x < Ґ
Параметры	x0 - параметр масштаба; sz - параметр формы
Плотность (функция вероятности)
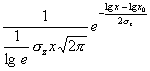
Математическое ожидание
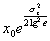
Дисперсия

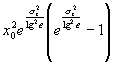
График f(x) при x₀ = 10, s_z = 0.8

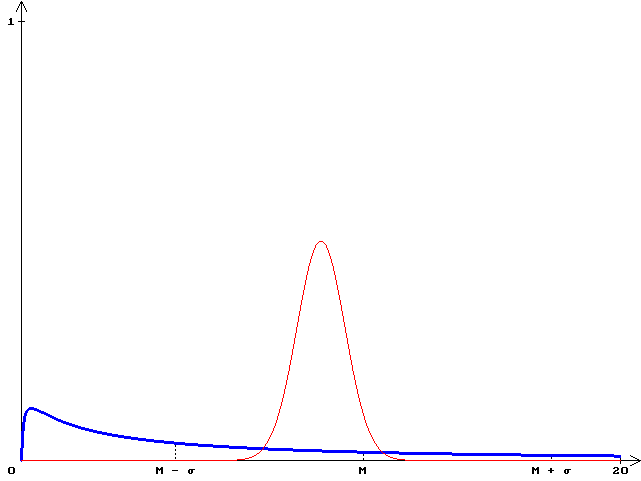
Пример логнормального распределения

Лазерный луч CD привода преодолевает некоторое расстояние перед считыванием с диска. Разобьем это расстояние на n участков. На каждом таком участке интенсивность луча лазера ослабевает (например, из-за наличия пыли в воздухе), т. е. имеем коэффициент потерь. Итоговый коэффициент потерь на всем расстоянии будет распределен по логнормальному закону.

Доказательство

Очевидно, что K = K₁ ґ ... ґ K_n. Поэтому lg K = lg K₁ + ... + lg K_n. Центральная предельная теорема гласит: "Если X₁, ..., X_n - независимые одинаково распределенные случайные величины, имеющие математическое ожидание и дисперсию, то при n ® Ґ закон распределения суммы неограниченно приближается к нормальному". Поэтому величина lg K будет распределена по нормальному закону, а это означает, что величина K, т.е. итоговый коэффициент потерь на всем расстоянии будет распределен по логнормальному закону