Распределение хи-квадрат

Если X_i независимые случайные величины, подчиненные нормальному распределению, у которых математическое ожидание равно нулю, а среднеквадратичное отклонение равно единице, то случайная величина 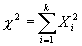подчиняется распределению c² (хи-квадрат) с k степенями свободы.

Область x	0 Ј x < Ґ
Параметры	k - параметр формы
Плотность (функция вероятности)
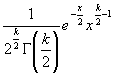
Математическое ожидание	k
Дисперсия	2k

График f(x) при k = 8

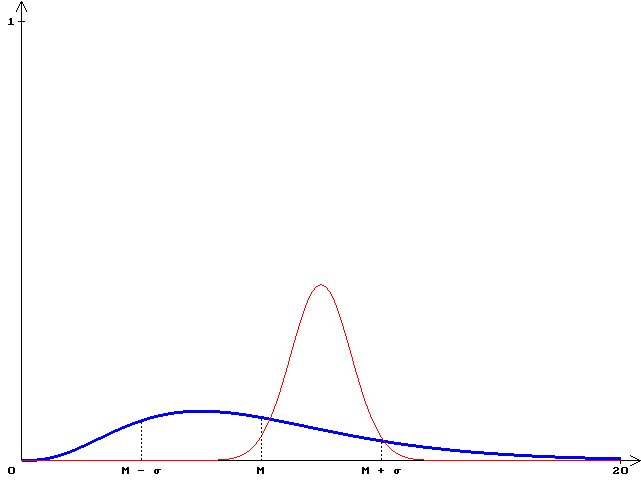
Пример распределения хи-квадрат

Пусть фирма выпустила новый процессор. Предположим, что каждые два года цена на этот процессор падает на 10%. Тогда количество таких процессоров, которые можно купить на фиксированную сумму может быть описано с помощью распределения хи-квадрат.

Доказательство

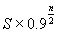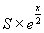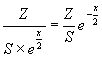Обозначим фиксированную сумму через Z. Пусть S - стартовая цена процессора. Тогда по прошествии n лет он будет стоить . Преобразуем полученное выражение: . Введем новую переменную: x = n ґ ln 0.9. Получим следующую формулу: . Количество процессоров, которые можно купить на фиксированную сумму, равно . Если закрыть глаза на коэффициенты, то полученная формула соответствует формуле плотности для распределения хи-квадрат при k = 2.